千橙工坊

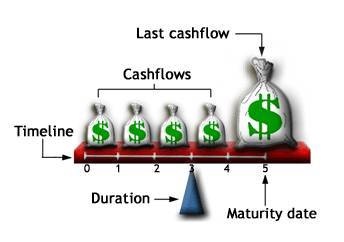
债券属性「久期」¹的本质是什么？

把债券相像成一系列排在跷跷板上的积木，每个积木代表一个现金流，现金流越多，积木越长。把这些木块按时间顺序从左到右排列在跷跷板上，大多数积木都是矮短的（每期的利息），最右边一块（到期还本付息）则擎天一柱比其他的高出很多。那么，债券的久期就是：
从跷跷板的左端到使跷跷板平衡的支点的距离。

-- 周召(via. 知乎) 这样形象描述.

久期就是投资者购买一个债券后，把本金和利息全都收回的加权时间总和。

$$ \begin{equation} D = \frac{\sum_{t=1}^T \frac{c_t}{(1+y)^t}\times t}{P} \text {, 麦考利久期的計算公式} \end{equation}$$

$$ MacD = \frac{\sum_{t=1}^T PV\left( c_t\right) \times t}{P} = \sum_{t=1}^T \left[ \frac{PV\left( C_t\right)}{P} \times t \right] \tag{2}$$

其中，
• MacD是久期，
• P是債券當前的市場價格，
• $PV\left( c_t\right)$ 是債券未來第t期可現金流（利息或資本）的現值，
• T是債券的到期時間。
• t為從當前到t時刻現金流發生的持續時間。
• y為債券的風險程度相適應的收益率。假設未來所有現金流的貼現率(discount ratio)都固定為y。可以理解为IRR 或者 YTM 或者 MWR.
需要指出的是在債券發行時以及發行後，都可以計算久期。計算發行時的久期，T（到期時間）等於債券的期限；計算發行後的久期，T（到期時間）小於債券的期限。

定理

1. 零息债券(Zero-coupon bonds)的久期等于它的到期时间
2. 直接债券(Direct bond)的久期小于或等于它的到期时间
3. 统一公债(Unified Bond)的久期等于$ 1+ {1\over Y} $，其中Y是计算现值的贴现率
4. 到期时间相同的条件下，息票率(Coupon rate)越高，久期越短
5. 息票率不变的条件下，到期时间越久，久期也越长
6. 其他条件不变的情况下，债券的到期收益率(YTM)越低，久期越长

久期既可以反应债权价格对于利率变化的敏感程度，也能够显示购买债权后，收回全部本金和利息的加权时间总和。

在实际的债券分析中，投资者更多地需要衡量债券价格变动比例对利率变化的敏感度，因此就有了修正久期这个概念。修正久期不同于久期，久期度量的是投资回收的平均时间，而修正久期实质上度量的是债券价格对收益率的一阶导数。
投资者除了用久期来衡量利率风险以外，还可以使用基点价值(Basis Point Value, BPV 或 DV01)。基点价值是指利率每变化一个基点（0.01 个百分点）时引起的债券价格变动的绝对额。因此，基点价值和修正久期最主要的不同体现在，基点价值衡量的是利率变动引起债券价格变动的绝对值，而修正久期衡量的是利率变动引起的债券价格变动的相对值。

債券凸性與馬考勒久期之間的關係